이진 트리와 트리의 순회, binary tree and traversal

08 Jul 2018

Reading time ~2 minutes

이진 트리, binary tree

이진 트리는 모든 노드가 최대 2개까지의 자식 노드만 가질 수 있는 트리

이진 트리 종류

1. 포화 이진 트리 (Full Binary Tree)

모든 노드가 두 개의 자식 노드를 가지며, 모든 잎 노드의 깊이가 같은 트리

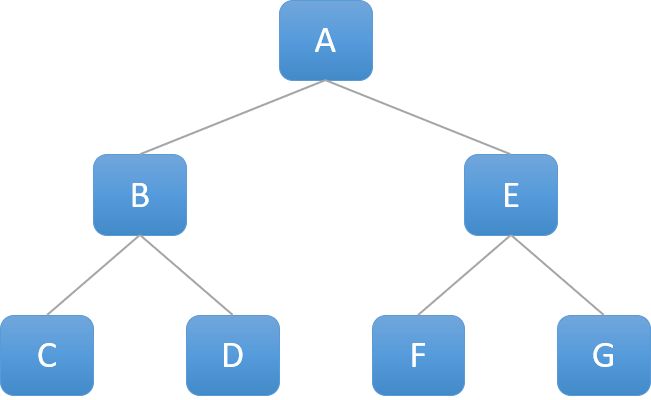
2. 완전 이진 트리 (Complete Binary Tree)

Leaf 노드가 왼쪽 부터 채워진 형태의 이진 트리

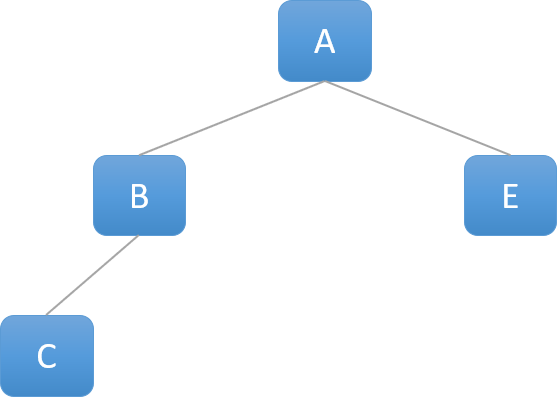
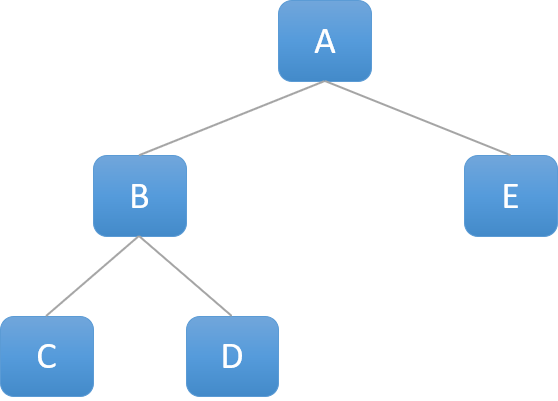
아래와 같은 형태는 완전 이진 트리가 아님! 왼쪽 부터 차례대로 채워지지가 않았으니까

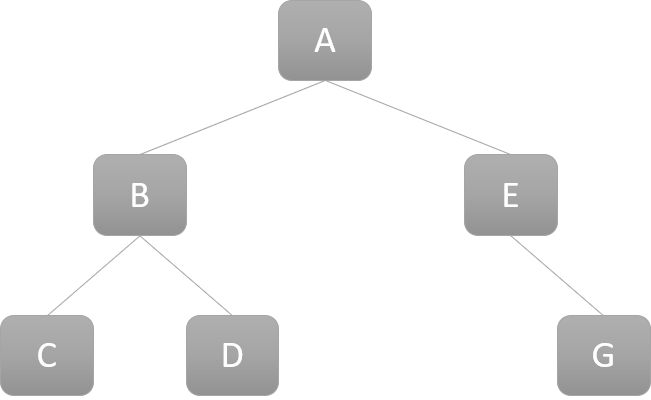
3. 높이 균형 트리 (Height Balanced Tree)

루트 노드의 왼쪽 하위 트리와 오른쪽 하위 트리의 높이 차이가 1 이상 나지 않는 이진 트리

4. 완전 높이 균형 트리 (Completely Height Balanced Tree)

루트 노드의 왼쪽, 오른쪽 하위 트리의 높이가 같은 이진 트리

이진 트리는 컴파일러나 탐색 등에 사용 되는 자료구조이기 때문에, 성능을 높이기 위해 가능한 완전한 모습으로 만드는 것이 중요.

이진 트리 순회 (Traversal)

1. 전위 순회 (Preorder Traversal)

전위 순회는 ‘루트 노드 - 왼쪽 하위 트리 - 오른쪽 하위 트리’ 순서로 트리를 순회하는 방법.

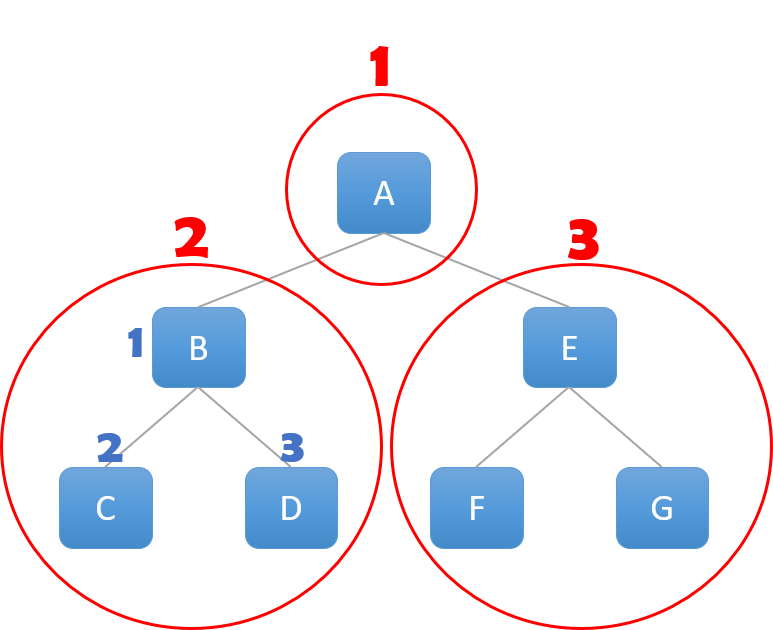
2. 중위 순회 (Inorder Traversal)

중위 순회는 ‘왼쪽 하위 트리 - 루트 노드 - 오른쪽 하위 트리’ 순서로 트리를 순회하는 방법.

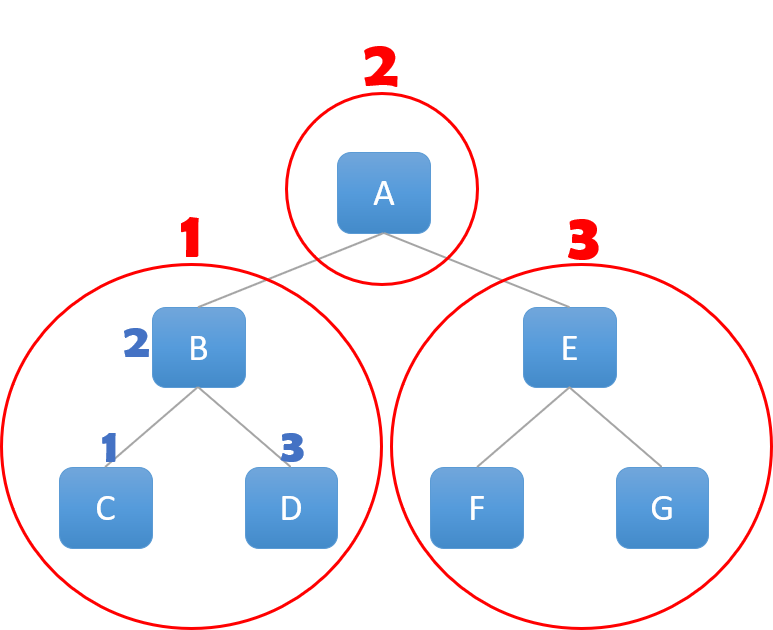
중위 순회는 대표적으로 ‘수식 트리’에 활용 .

3. 후위 순회 (Postorder Traversal)

후위 순회는 ‘왼쪽 하위 트리 - 오른쪽 하위 트리 - 루트 노드’ 순서로 트리를 순회하는 방법.

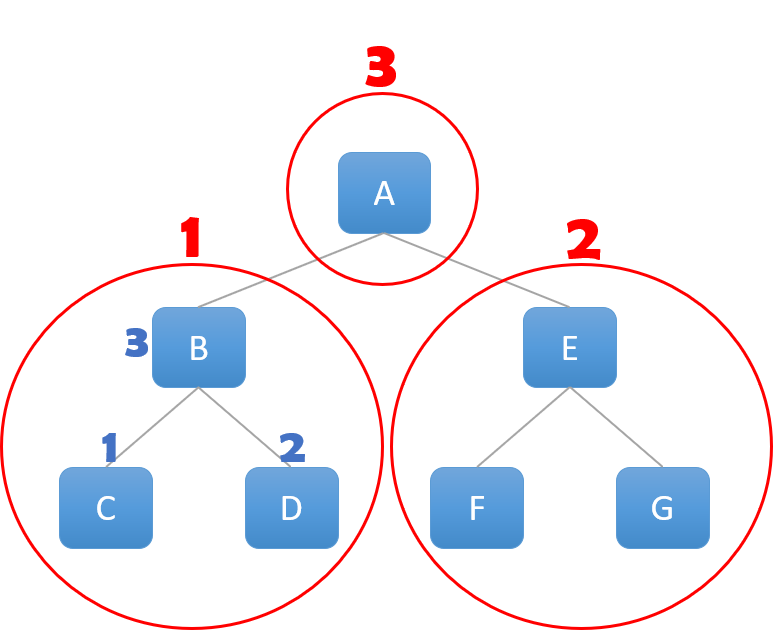
▼트리 순회 코드(java)▼

public class BinaryTree<E> {

	private static class Node<E> {
		Node<E> left;
		Node<E> right;
		E data;

		public Node(Node<E> left, Node<E> right, E data) {
			this.left = left;
			this.right = right;
			this.data = data;
		}
	}

	//전위순회
	public void preorder(Node<E> node) {
		if(node == null)
			return;

		System.out.println(node.data);

		preorder(node.left);

		preorder(node.right);
	}

	//중위순회
	public void inorder(Node<E> node) {
		if(node == null)
			return;

		inorder(node.left);

		System.out.println(node.data);

		inorder(node.right);
	}

	//후위순회
	public void postorder(Node<E> node) {
		if(node == null)
			return;

		postorder(node.left);

		postorder(node.right);

		System.out.println(node.data);
	}


	//이진트리 순회 테스트
	public static void main(String[] args) {

		BinaryTree<String> bt = new BinaryTree<String>();

		Node<String> C = new Node<String>(null, null, "C");
		Node<String> D= new Node<String>(null, null, "D");
		Node<String> F = new Node<String>(null, null, "F");
		Node<String> G = new Node<String>(null, null, "G");
		Node<String> B = new Node<String>(C, D, "B");
		Node<String> E = new Node<String>(F, G, "E");
		Node<String> A = new Node<String>(B, E, "A");

		System.out.println("------------ < 전위 순회 > ------------");
		bt.preorder(A);

		System.out.println("------------ < 중위 순회 > ------------");
		bt.inorder(A);

		System.out.println("------------ < 후위 순회 > ------------");
		bt.postorder(A);

	}

}

출력

------------ < 전위 순회 > ------------
A
B
C
D
E
F
G
------------ < 중위 순회 > ------------
C
B
D
A
F
E
G
------------ < 후위 순회 > ------------
C
D
B
F
G
E
A