자료구조 트리, datastructure tree

08 Jul 2018

Reading time ~2 minutes

『뇌를 자극하는 알고리즘』 을 바탕으로 공부한 내용입니다.

트리, Tree

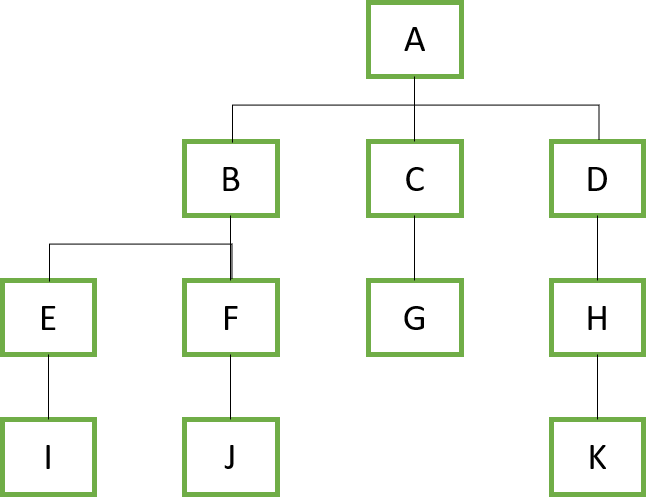
트리는 이름처럼 나무를 닮은 자료구조!
그런데 거꾸로 자라는 나무 모습을 하고 있다.

HTML의 DOM(Document Object Model)에서 트리 구조를 찾아 볼 수 있습니다.

1. 구성요소

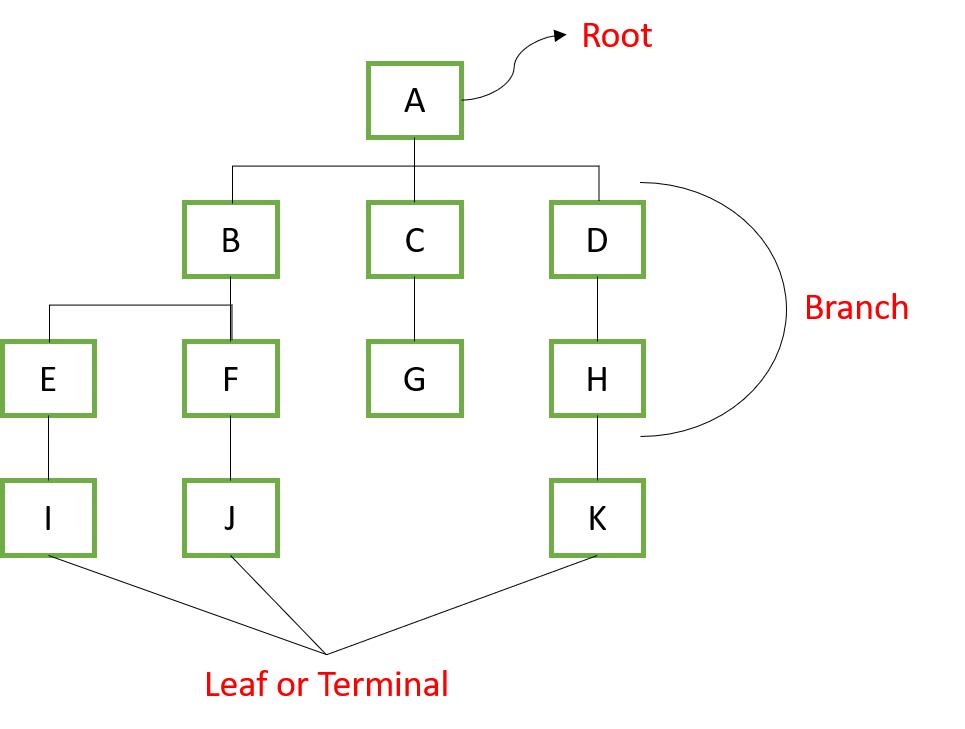
뿌리 (root)
가지 (branch)
잎 (leaf / terminal)

트리는 뿌리, 가지, 잎 세 가지로 구성되어 있다.

2. 용어

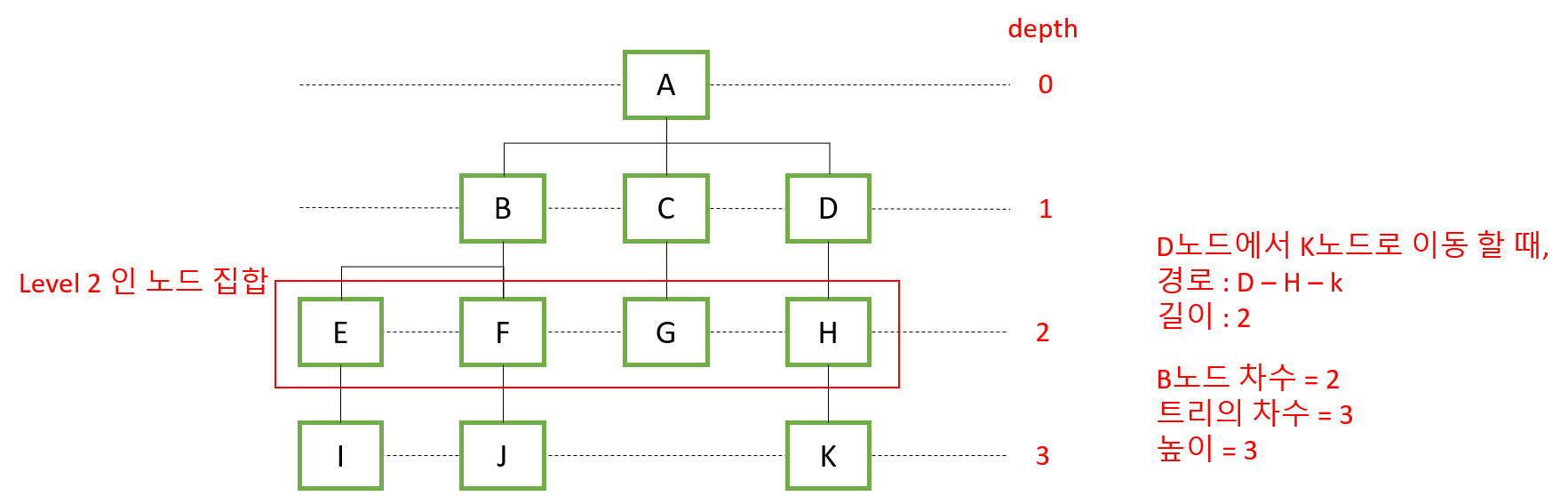
경로 (path) : 한 노드에서 다른 한 노드로 가는 길 사이에 놓여있는 노드들의 순서
- 길이 (length) : 경로를 따라 거쳐야 하는 노드의 개수
- 깊이 (depth) : 루트 노드로부터의 길이 루트의 깊이 = 0
  - Level : 길이가 같은 노드의 집합
  - 높이 (height) : 가장 깊은 곳에 있는 leaf노드의 깊이

차수 (degree)
- 노드의 차수 : 해당 노드의 자식 노드 개수
- 트리의 차수 : 트리에서 가장 많은 자식을 가지는 노드의 차수

3. 노드의 표현 : Left Child - Right Sibling

노드를 표현하는 방법 중에 “left child - right sibling” 이라는 방법이 있는데,

말 그대로 왼쪽에는 자식 노드, 오른쪽에는 형제 노드를 가리키도록 노드를 구성하는 방법이다.

▼left child - right sibling 방법으로 구현한 트리 (java)▼

public class Tree<E> {

	// 왼쪽 자식, 오른쪽 형제 형태의 노드
	public static class Node<E> {
		E data;
		Node<E> left_child;
		Node<E> right_sibling;

		public Node(E data) {
			this.data = data;
			left_child = null;
			right_sibling = null;
		}
	}

	// 노드 생성
	public void addChild(Node<E> parent, Node<E> child) {

		if (parent.left_child == null) {
			parent.left_child = child;
		} else {
			Node<E> node = parent.left_child;
			while (node.right_sibling != null) {
				node = node.right_sibling;
			}
			node.right_sibling = child;
		}

	}

	// 트리 삭제
	public void deleteTree(Node<E> root) {

		if (root.right_sibling != null)
			deleteTree(root.right_sibling);

		if (root.left_child != null)
			deleteTree(root.left_child);

		root.left_child = null;
		root.right_sibling = null;
		root.data = null;
		root = null;

	}

	// 검색
	public void readTree(Node<E> root, int depth) {
		if (root.data != null) {

			for (int i = 0; i < depth; i++) {
				System.out.print("   ");
			}

			System.out.println(root.data);

			if (root.left_child != null)
				readTree(root.left_child, depth + 1);

			if (root.right_sibling != null)
				readTree(root.right_sibling, depth);

		}

	}

}

Test_Tree.java

public class Test_Tree {

	public static void main(String[] args) {
		Tree<Character> myTree = new Tree<>();

		Tree.Node<Character> root = new Tree.Node<>('A');
		Tree.Node<Character> b = new Tree.Node<>('B');
		Tree.Node<Character> c = new Tree.Node<>('C');
		Tree.Node<Character> d = new Tree.Node<>('D');
		Tree.Node<Character> e = new Tree.Node<>('E');
		Tree.Node<Character> f = new Tree.Node<>('F');
		Tree.Node<Character> g = new Tree.Node<>('G');
		Tree.Node<Character> h = new Tree.Node<>('H');
		Tree.Node<Character> i = new Tree.Node<>('I');
		Tree.Node<Character> j = new Tree.Node<>('J');
		Tree.Node<Character> k = new Tree.Node<>('K');


		myTree.addChild(root, b);
		myTree.addChild(b, e);
		myTree.addChild(e, i);
		myTree.addChild(b, f);
		myTree.addChild(f, j);


		myTree.addChild(root, c);
		myTree.addChild(c, g);

		myTree.addChild(root, d);
		myTree.addChild(d, h);
		myTree.addChild(h, k);

		//출력
		myTree.readTree(root, 0);

		myTree.deleteTree(root);

		System.out.println("----------- <delete tree> ------------");


	}

}

출력 결과

A
   B
      E
         I
      F
         J
   C
      G
   D
      H
         K
----------- <delete tree> ------------